2017-2018 Petrozavodsk Winter Training Camp, Saratov SU Contest 补题记录（8 / 12）

发表于 更新于 分类于 本文字数： 20k 阅读时长 ≈ 18 分钟

2017-2018 ptz Saratov 补题记录

A. Three Arrays

tag

  • 二分
  • 思维

题意

给定长为 na,nb,ncna, nb, nc 的数列 a,b,ca, b, c ，保证 a,b,ca, b, c 均单调不降，求数对 (i,j,k)(i, j, k) 的数量，其中 (i,j,k)(i, j, k) 满足 ∣ai−bj∣≤d,∣bj−ck∣≤d,∣ai−ck∣≤d|a_i - b_j| \leq d, |b_j - c_k| \leq d, |a_i - c_k| \leq d 。
其中 1≤n≤5⋅105,−109≤ai,bi,ci≤1091 \leq n \leq 5 \cdot 10^5, - 10^9 \leq a_i, b_i, c_i \leq 10^9 。

思路

枚举 ai,bj,cka_i, b_j, c_k 中的最小值，得到另两个数的范围，直接统计贡献即可，注意多个最小值的情况不重复算。
复杂度 O(n⋅logn)O(n \cdot logn) 。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
using namespace std;

using ll=long long;

const int INF=0x3f3f3f3f;
const int N=5e5+5;

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);

    int d,na,nb,nc;
    while(cin>>d>>na>>nb>>nc){
        vector<int> a(na,0),b(nb,0),c(nc,0),app;
        for(auto &x:a) cin>>x;
        for(auto &x:b) cin>>x;
        for(auto &x:c) cin>>x;

        ll ans=0;
        for(int i=0;i<na;i++){
            int lenb=upper_bound(b.begin(),b.end(),a[i]+d)-lower_bound(b.begin(),b.end(),a[i]);
            int lenc=upper_bound(c.begin(),c.end(),a[i]+d)-lower_bound(c.begin(),c.end(),a[i]);
            ans+=1ll*lenb*lenc;
        }
        for(int i=0;i<nb;i++){
            int lena=upper_bound(a.begin(),a.end(),b[i]+d)-lower_bound(a.begin(),a.end(),b[i]+1);
            int lenc=upper_bound(c.begin(),c.end(),b[i]+d)-lower_bound(c.begin(),c.end(),b[i]);
            ans+=1ll*lena*lenc;
        }
        for(int i=0;i<nc;i++){
            int lena=upper_bound(a.begin(),a.end(),c[i]+d)-lower_bound(a.begin(),a.end(),c[i]+1);
            int lenb=upper_bound(b.begin(),b.end(),c[i]+d)-lower_bound(b.begin(),b.end(),c[i]+1);
            ans+=1ll*lena*lenb;
        }
        cout<<ans<<'\n';
    }

    return 0;
}

C. Cover the Paths

tag

  • 贪心

题意

给定树上若干条路径，求最小的点集使得每条路径都至少被一个点覆盖。
树的大小与路径数 1≤n,m≤1051 \leq n, m \leq 10^5 。

思路

若在序列上则是经典区间覆盖问题，放在树上考虑类似的贪心，对所有路径的 lcalca 按深度排序后贪心放即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<bits/stdc++.h>
using namespace std;

using ll=long long;

const int N=1e5+5;

set<int> st[N];

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    
    int n;
    cin>>n;

    vector<vector<int>> e(n,vector<int>(0));
    for(int i=1,x,y;i<n;i++){
        cin>>x>>y;
        x--,y--;
        e[x].push_back(y);
        e[y].push_back(x);
    }

    int m;
    cin>>m;

    vector<int> ans(n,0),vis(n,0);
    for(int i=0;i<m;i++){
        int u,v,lca;
        cin>>u>>v;
        u--,v--;
        if(u==v){
            ans[u]=1;
            continue;
        }
        st[u].insert(i);
        st[v].insert(i);
    }

    function<void(int,int)> dfs=[&](int x,int fa){
        int flag=0;
        for(auto v:e[x]){
            if(v==fa) continue;
            dfs(v,x);
            if(st[v].size()>st[x].size()) st[x].swap(st[v]);
            for(auto val:st[v]){
                if(st[x].find(val)!=st[x].end()) flag=1;
                st[x].insert(val);
            }
        }
        if(ans[x]){
            st[x].clear();
            return;
        }
        if(flag){
            ans[x]=1;
            st[x].clear();
        }
    };

    dfs(0,0);

    int sum=0;
    for(int i=0;i<n;i++) sum+=ans[i];
    
    cout<<sum<<'\n';
    for(int i=0;i<n;i++) if(ans[i]) cout<<i+1<<' ';

    return 0;
}

D. Elevator

tag

  • DP
  • 线段树

题意

给定 nn 个人的到达时间 tit_i 与目标层数 aia_i ， 00 时刻电梯在楼层 00 ，电梯每次运送当前的若干人再回到起点，电梯每上升或下降一层花费一个单位时间，求电梯运送完所有人并回到起点花费的最小时间。
其中 1≤n≤2⋅105,1≤ti,ai≤109,ti<ti+1(1≤i<n)1 \leq n \leq 2 \cdot 10^5, 1 \leq t_i, a_i \leq 10^9, t_i < t_{i+1} (1 \leq i < n) 。

思路

记 dpidp_i 为运完前i个人并回到起点的最小花费，则有朴素的转移：

{dpi=min(max(dpj,ti)+2⋅max(aj+1,...,ai))(0≤j<i)dp[0]=0\begin{cases} dp_i = min(max(dp_j, t_i) + 2 \cdot max(a_{j+1}, ..., a_i))(0 \leq j <i)\\ dp[0] = 0 \end{cases}

显然可以套两个线段树优化。
复杂度 O(n⋅logn)O(n \cdot logn) 。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include<bits/stdc++.h>
using namespace std;

using ll=long long;

const ll INF=0x3f3f3f3f3f3f3f3f;

const int N=2e5+5;

struct tree{
    int l[N<<2];
    int r[N<<2];
    ll lz[N<<2];
    ll minn[N<<2];
    void pushup(int x){
        minn[x]=min(minn[x<<1],minn[x<<1|1]);
    }
    void build(int x,int L,int R){
        l[x]=L;
        r[x]=R;
        lz[x]=minn[x]=0;
        if(L==R) return;
        int mid=L+R>>1;
        build(x<<1,L,mid);
        build(x<<1|1,mid+1,R);
        return;
    }
    void pushdown(int x){
        if(lz[x]){
            ll val=lz[x];
            minn[x<<1]+=val;
            lz[x<<1]+=val;
            minn[x<<1|1]+=val;
            lz[x<<1|1]+=val;
            lz[x]=0;
        }
    }
    void add(int x,int L,int R,ll val){
        if(l[x]>=L&&r[x]<=R){
            minn[x]+=val;
            lz[x]+=val;
            return;
        }
        pushdown(x);
        if(r[x<<1]>=L) add(x<<1,L,R,val);
        if(l[x<<1|1]<=R) add(x<<1|1,L,R,val);
        pushup(x);
        return;
    }
    ll search(int x,int L,int R){
        if(L>R) return INF;
        if(l[x]>=L&&r[x]<=R) return minn[x];
        pushdown(x);
        ll res=INF;
        if(r[x<<1]>=L) res=min(res,search(x<<1,L,R));
        if(l[x<<1|1]<=R) res=min(res,search(x<<1|1,L,R));
        return res;
    }
}tr[2];

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);

    int n;
    while(cin>>n){
        vector<int> t(n+5,0),a(n+5,0);
        for(int i=1;i<=n;i++) cin>>t[i]>>a[i];

        tr[0].build(1,1,n);
        tr[1].build(1,1,n);

        vector<ll> dp(n+5,INF);
        vector<int> st;
        st.push_back(0);
        int pos=1;
        dp[0]=0;
        for(int i=1;i<=n;i++){
            while(st.back()&&a[st.back()]<=a[i]){
                int p=st.back();
                st.pop_back();
                tr[0].add(1,st.back()+1,p,-2ll*a[p]);
                tr[1].add(1,st.back()+1,p,-2ll*a[p]);
            }
            tr[0].add(1,st.back()+1,i,2ll*a[i]);
            tr[1].add(1,st.back()+1,i,2ll*a[i]);
            st.push_back(i);
            tr[0].add(1,i,i,dp[i-1]);
            while(pos<=i&&dp[pos-1]<t[i]) pos++;
            if(pos<=i&&dp[pos-1]>=t[i]) dp[i]=min(dp[i],tr[0].search(1,pos,i));
            dp[i]=min(dp[i],tr[1].search(1,1,pos-1)+t[i]);
        }

        cout<<dp[n]<<"\n";
    }

    return 0;
}

F. GCD

tag

  • 随机化
  • 前缀和

挺 nb 的题。

题意

给定长为 nn 的数列 aa ，最多删去 kk 个数使得剩下数 gcdgcd 最大，求这个最大值。
其中 2≤n≤105,0≤k≤n2,1≤ai≤10182 \leq n \leq 10^5, 0 \leq k \leq \frac{n}{2}, 1 \leq a_i \leq 10^{18} 。

思路

考虑从 aa 中随机选一个数 SS，那么 SS 有 n−kn\frac{n - k}{n} 的概率是最后留在答案数组中的，多取几次 SS 对每个符合要求的 SS 的因子取 maxmax 即可。
假设当前选定了数 SS ，记录 cnticnt_i 为因子 ii 在数列中出现的次数，初始对于每个 gi=gcd(S,ai)g_i = gcd(S, a_i) 令 cntgi++cnt_{g_i}++ 。
之后从大往小遍历 SS 的因子 jj ，可以将 cntjcnt_j 加至 cntjpricnt{\frac{j}{pr_i}} 上， pripr_i 为 SS 的第 ii 个质因子，这类似做一个高维前缀和的过程，对于 SS 的每个质因子都做一遍可以得到 SS 的每个因子在数列中出现的次数。
选出现次数大于等于 n−kn - k 的因子并取 maxmax 即可。
由于 101810^{18} 内的数 SS 最多有 S13S^\frac{1}{3} 个因子，最多有 1616 个不同的质因子，所以做前缀和处理 cntcnt 部分的复杂度为 O(S13⋅t)O(S^\frac{1}{3} \cdot t) ， tt 为 SS 中不同的质因子个数。
复杂度 O(T⋅(max(ai)13⋅t+n))O(T \cdot (max(a_i)^{\frac{1}{3}} \cdot t + n)) ， TT 为重复选取 SS 的次数， tt 为 SS 中不同的质因子个数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
#include<bits/stdc++.h>
using namespace std;

using ll=long long;

namespace PR{
    set<long long> res;
    long long max_factor;
    long long gcd(long long a,long long b){
        if(b==0) return a;
        return gcd(b,a%b);
    }
    long long power(long long a,long long b,long long mod){
        long long res=1;
        while(b){
            if(b&1) res=(__int128)res*a%mod;
            a=(__int128)a*a%mod;
            b>>=1;
        }
        return res;
    }
    int Miller_Rabin(long long p){
        if(p<2) return 0;
        if(p==2) return 1;
        if(p==3) return 1;
        long long d=p-1,r=0;
        while(!(d&1)) ++r,d>>=1;
        for(long long k=0;k<10;++k){
            long long a=rand()%(p-2)+2;
            long long x=power(a,d,p);
            if(x==1||x==p-1) continue;
            for(int i=0;i<r-1;++i){
                x=(__int128)x*x%p;
                if(x==p-1) break;
            }
            if(x!=p-1) return 0;
        }
        return 1;
    }
    long long Pollard_Rho(long long x){
        long long s=0,t=0;
        long long c=(long long)rand()%(x-1)+1;
        int step=0,goal=1;
        long long val=1;
        for(goal=1;;goal*=2,s=t,val=1){
            for(step=1;step<=goal;++step){
                t=((__int128)t*t+c)%x;
                val=(__int128)val*abs(t-s)%x;
                if((step%127)==0){
                    long long d=gcd(val,x);
                    if(d>1) return d;
                }
            }
            long long d=gcd(val,x);
            if(d>1) return d;
        }
    }
    void fac(long long x){
        if(x<=max_factor||x<2) return;
        if(Miller_Rabin(x)){
            res.insert(x);
            return;
        }
        long long p=x;
        while(p>=x) p=Pollard_Rho(x);
        fac(x/p),fac(p);
    }
    void get_fac(long long x){
        srand((unsigned)time(0));
        res.clear();
        fac(x);
    }
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);

    int n,k;
    cin>>n>>k;

    vector<ll> a(n,0);
    for(auto &x:a) cin>>x;

    auto solve=[&](ll S){
        PR::get_fac(S);
        map<ll,int> mp;
        for(auto x:a) mp[__gcd(S,x)]++;
        for(auto g:PR::res){
            for(auto it=mp.rbegin();it!=mp.rend();it++){
                auto [x,cnt]=(*it);
                if(x%g==0) mp[x/g]+=cnt;
            }
        }
        ll res=0;
        for(auto [val,cnt]:mp) if(cnt>=n-k) res=max(res,val);
        return res;
    };

    ll ans=1;
    vector<int> p(n,0);
    iota(p.begin(),p.end(),0);
    srand(time(0));
    for(int i=0;i<60;i++){
        random_shuffle(p.begin(),p.end());
        ans=max(ans,solve(a[p[1ll*rand()*rand()*rand()%n]]));
    }

    cout<<ans;

    return 0;
}

G. Berland Post

tag

  • 二分
  • 差分约束

题意

给定 nn 个点 mm 个限制 oai+di≤obi+To_{a_i} + d_i \leq o_{b_i} + T 一些 oio_i 确定一些不定，求最小的非负实数 TT 。
其中 1≤n≤103,0≤m≤2⋅103,−105≤oi≤105,1≤ai,bi≤n,1≤di≤1001 \leq n \leq 10^3, 0 \leq m \leq 2 \cdot 10^3, - 10^5 \leq o_i \leq 10^5, 1 \leq a_i, b_i \leq n, 1 \leq d_i \leq 100 ， oio_i 不定表示为 ?? 。

思路

显然对于 TT 的取值可以二分。
二分后将每个限制表示为 disbi≥disai+di−Tdis_{b_i} \geq dis_{a_i} + d_i - T ，对于确定的 oio_i 可以表示为限制 disoi≤oi,disoi≥oidis_{o_i} \leq o_i, dis_{o_i} \geq o_i 。跑一遍差分约束即可。
复杂度 O(log(109)⋅n)O(log(10^9) \cdot n) 。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include<bits/stdc++.h>
using namespace std;

using ll=long long;
using pid=pair<int,double>;

const double INF=1e9;

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);

    int n,m;
    while(cin>>n>>m){
        vector<string> str(n,"");
        vector<int> d(n,0);
        vector<array<int,3>> edge(m);
        for(int i=0;i<n;i++){
            cin>>str[i];
            if(str[i]=="?") d[i]=-INF;
            else d[i]=stoi(str[i]);
        }
        for(auto &[u,v,w]:edge){
            cin>>u>>v>>w;
            u--,v--;
        }

        vector<double> dis(n+1,-INF);
        auto check=[&](double mid){
            vector<int> vis(n+1,0);
            vector<vector<pid>> e(n+1,vector<pid>(0));
            for(int i=0;i<n;i++) if(d[i]!=-INF){
                e[n].push_back({i,d[i]});
                e[i].push_back({n,-d[i]});
            }
            for(auto [u,v,w]:edge) e[u].push_back({v,w-mid});
            for(int i=0;i<n;i++) dis[i]=-INF;
            dis[n]=0;
            queue<int> q;
            q.push(n);
            for(int i=0;i<n;i++) q.push(i);
            while(!q.empty()){
                int x=q.front();
                q.pop();
                for(auto [v,w]:e[x]){
                    if(dis[v]<dis[x]+w){
                        dis[v]=dis[x]+w;
                        vis[v]++;
                        if(vis[v]>n) return 0;
                        q.push(v);
                    }
                }
            }
            return 1;
        };

        double l=0,r=1e9;
        for(int i=0;i<60;i++){
            double mid=(l+r)/2;
            if(check(mid)) r=mid;
            else l=mid;
        }

        cout<<fixed<<setprecision(9)<<r<<"\n";
        check(r);
        for(int i=0;i<n;i++) cout<<dis[i]<<" \n"[i+1==n];
    }

    return 0;
}

J. Subsequence Sum Queries

tag

  • 分治
  • DP

题意

长为 nn 的数列 aa 与数 mm ， qq 次询问，每次询问 [l,r][l, r] 内和为 mm 的倍数的子序列个数。
其中 1≤n≤2⋅105,1≤m≤20,0≤ai≤109,1≤q≤2⋅1051 \leq n \leq 2 \cdot 10^5, 1 \leq m \leq 20, 0 \leq a_i \leq 10^9, 1 \leq q \leq 2 \cdot 10^5 。

思路

显然可以有线段树合并区间背包的方法，但复杂度为 O(n⋅m2⋅logn)O(n \cdot m^2 \cdot logn) 显然寄了。除非像 Pedestrian1 一样卡常。
考虑线段树合并背包存在的问题，对于不同的询问其实有多次合并区间的操作是重复的，可以类比整体二分将询问离线下来分治处理，对于询问 [li,ri][l_i, r_i] ，当前处理到的区间为 [L,R][L, R] ，令 mid=(L+R)/2mid = (L + R) / 2 ，若 ri≤midr_i \leq mid ，则递归到左区间再处理询问，若 li≥mid+1l_i \geq mid+1 则递归到右区间再处理询问，对于剩下的询问 O(n)O(n) 预处理 dpli,j,dpri,jdpl_{i,j}, dpr_{i,j} 表示区间 [i,mid][i, mid] 与区间 [mid+1,i][mid+1, i] 内和在模 mm 意义下为 jj 的子序列个数，对于每个询问 O(m)O(m) 地合并即可。
总复杂度为 O(n⋅m⋅logn+m⋅q)O(n \cdot m \cdot logn + m \cdot q) 。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<bits/stdc++.h>
using namespace std;

using ll=long long;

const int mod=1e9+7;
const int N=2e5+5;

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);

    int n,m;
    cin>>n>>m;

    vector<int> a(n+5,0);
    for(int i=1;i<=n;i++) cin>>a[i];

    int q;
    cin>>q;
    vector<int> ql(q+5,0),qr(q+5,0);
    for(int i=1;i<=q;i++) cin>>ql[i]>>qr[i];

    vector<array<int,20>> dp(n+5);
    vector<int> qry,ans(q+5,0);
    for(int i=1;i<=q;i++) qry.push_back(i);
    function<void(int,int,vector<int>&)> calc=[&](int l,int r,vector<int> &qry){
        if(qry.empty()) return;
        if(l==r){
            if(a[l]%m==0) for(auto x:qry) ans[x]=(ans[x]+1)%mod;
            return;
        }
        int mid=l+r>>1;
        vector<int> qry1,qry2,qry3;
        for(auto x:qry){
            if(qr[x]<=mid) qry1.push_back(x);
            else if(ql[x]>=mid+1) qry2.push_back(x);
            else qry3.push_back(x);
        }
        calc(l,mid,qry1);
        calc(mid+1,r,qry2);
        for(int i=l;i<=r;i++)
            for(int j=0;j<m;j++) dp[i][j]=0;
        for(int i=mid;i>=l;i--){
            dp[i][a[i]%m]=(dp[i][a[i]%m]+1)%mod;
            if(i+1<=mid){
                for(int j=0;j<m;j++)
                    dp[i][(j+a[i]%m)%m]=(dp[i][(j+a[i]%m)%m]+dp[i+1][j])%mod;
                for(int j=0;j<m;j++)
                    dp[i][j]=(dp[i][j]+dp[i+1][j])%mod;
            }
        }
        for(int i=mid+1;i<=r;i++){
            dp[i][a[i]%m]=(dp[i][a[i]%m]+1)%mod;
            if(i-1>=mid+1){
                for(int j=0;j<m;j++)
                    dp[i][(j+a[i]%m)%m]=(dp[i][(j+a[i]%m)%m]+dp[i-1][j])%mod;
                for(int j=0;j<m;j++)
                    dp[i][j]=(dp[i][j]+dp[i-1][j])%mod;
            }
        }
        for(auto x:qry3){
            for(int i=0;i<m;i++) ans[x]=(ans[x]+1ll*dp[ql[x]][i]*dp[qr[x]][(m-i)%m]%mod)%mod;
            ans[x]=(ans[x]+dp[ql[x]][0])%mod;
            ans[x]=(ans[x]+dp[qr[x]][0])%mod;
        }
        return;
    };

    calc(1,n,qry);

    for(int i=1;i<=q;i++) cout<<(ans[i]+1)%mod<<'\n';

    return 0;
}

K. Consistent Occurrences

tag

  • AC自动机
  • 分治

题意

给定长为 nn 的小写字符串 ss ， qq 次询问每次询问串 tt 在 ss 中出现次数。（出现的 tt 之间不能重叠）
其中 1≤n,q≤105,∑∣t∣≤1051 \leq n, q \leq 10^5, \sum|t| \leq 10^5 。

思路

考虑根号分治，对于长度大于等于 n\sqrt{n} 的串 tt ，直接暴力跑 kmpkmp 即可，每次匹配成功则将匹配指针清空。
对于长度小于 n\sqrt{n} 的所有串 tt ，一起建一个 ACAC 机暴力匹配即可，在 ACAC 机的每个节点记录 dpi,0/1dp_{i,0/1} 表示这个节点被匹配的次数与最后一个被匹配到的位置，在 ACAC 机上每走一步就暴力跳 failfail 更新 dpdp 值即可。
总复杂度 O(n⋅n)O(n \cdot \sqrt{n}) 。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
const int M=26;

struct Trie{
    int tot;
    int nex[N][M];
    int fail[N];
    int len[N];
    int pos[N];
    int ans[N][2];
    void clear(){
        tot=0;
        fail[0]=len[0]=ans[0][0]=0;
        ans[0][1]=-1;
        memset(nex[0],0,sizeof(nex[0]));
    }
    Trie(){
        clear();
    }
    int addnode(){
        tot++;
        fail[tot]=len[tot]=ans[tot][0]=0;
        ans[tot][1]=-1;
        memset(nex[tot],0,sizeof(nex[tot]));
        return tot;
    }
    void insert(string s,int ind){
        int u=0;
        for(int i=0;i<s.size();i++){
            int w=s[i]-'a';
            if(!nex[u][w]) nex[u][w]=addnode();
            len[nex[u][w]]=len[u]+1;
            u=nex[u][w];
        }
        pos[ind]=u;
    }
    void buildfail(){
        queue<int> q;
        for(int i=0;i<M;i++) if(nex[0][i]) q.push(nex[0][i]);
        while(!q.empty()){
            int u=q.front();
            q.pop();
            for(int i=0;i<M;i++){
                if(nex[u][i]){
                    int v=nex[u][i];
                    fail[v]=nex[fail[u]][i];
                    q.push(nex[u][i]);
                }
                else nex[u][i]=nex[fail[u]][i];
            }
        }
    }
}acam;

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);

    int n,q;
    cin>>n>>q;
    int blo=sqrt(n);

    string s;
    cin>>s;

    vector<string> t(q,"");
    vector<int> ans(q,0),fail(n,0);
    for(int i=0;i<q;i++){
        cin>>t[i];
        if(t[i].size()<=blo) acam.insert(t[i],i);
        else if(t[i].size()<=n){
            fail[0]=-1;
            for(int j=1;j<t[i].size();j++){
                for(int k=fail[j-1];;k=fail[k]){
                    if(t[i][k+1]==t[i][j]){
                        fail[j]=k+1;
                        break;
                    }
                    else if(k==-1){
                        fail[j]=-1;
                        break;
                    }
                }
            }
            int now=-1;
            for(int j=0;j<n;j++){
                while(now!=-1&&t[i][now+1]!=s[j]) now=fail[now];
                if(t[i][now+1]==s[j]) now++;
                if(now+1==t[i].size()){
                    ans[i]++;
                    now=-1;
                }
            }
        }
    }
    acam.buildfail();

    int now=0;
    for(int i=0;i<n;i++){
        now=acam.nex[now][s[i]-'a'];
        for(int p=now;p;p=acam.fail[p]){
            if(acam.ans[p][1]+acam.len[p]<=i){
                acam.ans[p][0]++;
                acam.ans[p][1]=i;
            }
        }
    }

    for(int i=0;i<q;i++){
        if(t[i].size()<=blo) cout<<acam.ans[acam.pos[i]][0]<<"\n";
        else cout<<ans[i]<<"\n";
    }

    return 0;
}

L. Increasing Costs

tag

  • 拓扑排序

题意

给定 nn 个点 mm 条边的无向连通图，对每条边求删去这条边后 11 号点到多少个点的最短路会发生改变。
其中 2≤n≤2⋅105,n−1≤m≤2⋅105,1≤wi≤1092 \leq n \leq 2 \cdot 10^5, n - 1 \leq m \leq 2 \cdot 10^5, 1 \leq w_i \leq 10^9 ，wiw_i 为边权。

思路

首先从 11 号点跑一次最短路，只保留 disvi=disui+widis_{v_i} = dis_{u_i} + w_i 边并定向，其余边答案为 00 ，处理完后新图即为一个 DAGDAG ， 11 号点为唯一一个入度为 00 的点。
对于处理完后的边分两类：

  • 边指向的点入度为 11 ，则边的答案对应该边终点的答案
  • 边指向的点入度不为 11 ，则改边的答案为 00

问题即转换为对于每个点 xx 求如下操作后的被染色的点的数量：

  • 初始将 xx 染色
  • 若一个点的所有指向它的节点都被染色，则它也被染色

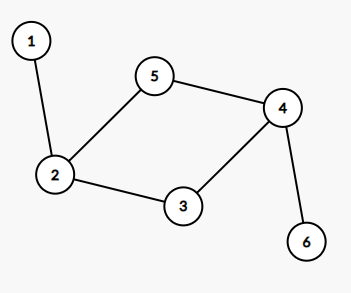
例如，下图每个节点的答案为： 6,5,1,2,1,16, 5, 1, 2, 1, 1

令 S(x)S(x) 为从 xx 节点开始染色最后被染色的点的集合，显然可以得到两个不同的集合 S(x),S(y)S(x), S(y) 之间只有包含和交集为空两种关系，即为一个树形结构，因为只有 11 号点入度为 00 ，所以所有集合之间必定构成一颗树。（可以反证或者参考2022牛客多校1J）
考虑如何构建这棵树：

  • 11 号点为根
  • 若 xx 入度为 11 ，则 xx 的父节点为唯一指向它的点
  • 若 xx 入度不为 11 ，则 xx 的父节点为指向它的所有点在构造出来的树上的 lcalca

具体构造时从 11 号点开始拓扑一遍即可，节点 xx 被遍历到时所有指向它的点一定已经完成构造，倍增处理 lcalca 即可。
总复杂度 O(n⋅logn)O(n \cdot logn) 。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#include<bits/stdc++.h>
using namespace std;

using ll=long long;
using pii=pair<int,int>;
using pll=pair<ll,ll>;

const ll INF=0x3f3f3f3f3f3f3f3f;

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);

    int n,m;
    cin>>n>>m;

    vector<array<int,3>> edge(m);
    vector<vector<pii>> e(n,vector<pii>(0));
    for(auto &[u,v,w]:edge){
        cin>>u>>v>>w;
        u--,v--;
        e[u].push_back({v,w});
        e[v].push_back({u,w});
    }

    vector<ll> dis(n,INF);
    auto dij=[&](){
        priority_queue<pll,vector<pll>,greater<pll>> q;
        dis[0]=0;
        q.push({dis[0],0});
        while(!q.empty()){
            auto [d,x]=q.top();
            q.pop();
            if(d>dis[x]) continue;
            for(auto [v,w]:e[x]){
                if(dis[v]>dis[x]+w){
                    dis[v]=dis[x]+w;
                    q.push({dis[v],v});
                }
            }
        }
    };

    dij();

    vector<int> in(n,0),sz(n,1),dep(n,0);
    vector<array<int,18>> f(n);
    vector<vector<int>> ed(n,vector<int>(0)),fa(n,vector<int>(0));
    for(int i=0;i<n;i++) e[i].clear();
    for(auto [u,v,w]:edge){
        if(dis[v]==dis[u]+w){
            fa[v].push_back(u);
            e[u].push_back({v,1});
            in[v]++;
        }
        else if(dis[u]==dis[v]+w){
            fa[u].push_back(v);
            e[v].push_back({u,1});
            in[u]++;
        }
    }

    auto get_lca=[&](int x,int y){
        if(x==y) return x;
        if(dep[x]<dep[y]) swap(x,y);
        for(int i=17;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
        for(int i=17;i>=0;i--) if(f[x][i]!=f[y][i]){
            x=f[x][i];
            y=f[y][i];
        }
        while(x!=y){
            x=f[x][0];
            y=f[y][0];
        }
        return x;
    };

    queue<int> q;
    for(int i=0;i<n;i++) if(!in[i]) q.push(i);
    while(!q.empty()){
        int x=q.front();
        q.pop();
        for(auto [v,w]:e[x]){
            in[v]--;
            if(!in[v]){
                if(fa[v].size()==1){
                    dep[v]=dep[x]+1;
                    ed[x].push_back(v);
                    f[v][0]=x;
                    for(int i=1;i<18;i++) f[v][i]=f[f[v][i-1]][i-1];
                }
                else{
                    int lca=fa[v].back();
                    fa[v].pop_back();
                    while(fa[v].size()){
                        lca=get_lca(lca,fa[v].back());
                        fa[v].pop_back();
                    }
                    dep[v]=dep[lca]+1;
                    ed[lca].push_back(v);
                    f[v][0]=lca;
                    for(int i=1;i<18;i++) f[v][i]=f[f[v][i-1]][i-1];
                }
                q.push(v);
            }
        }
    }

    function<void(int)> dfs=[&](int x){
        for(auto v:ed[x]){
            dfs(v);
            sz[x]+=sz[v];
        }
    };

    dfs(0);

    for(auto [u,v,w]:edge){
        if(dis[v]==dis[u]+w) in[v]++;
        else if(dis[u]==dis[v]+w) in[u]++;
    }
    for(auto [u,v,w]:edge){
        if(dis[v]==dis[u]+w){
            if(in[v]==1) cout<<sz[v]<<"\n";
            else cout<<"0\n";
        }
        else if(dis[u]==dis[v]+w){
            if(in[u]==1) cout<<sz[u]<<"\n";
            else cout<<"0\n";
        }
        else cout<<"0\n";
    }

    return 0;
}